第 258 场周赛 5870. 每棵子树内缺失的最小基因值
最后一题没做出来,思路错误, rank 318
Desciption
有一棵根节点为 0 的 家族树 ,总共包含 n 个节点,节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ,其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ,所以 parents[0] == -1 。
总共有 105 个基因值,每个基因值都用 闭区间 [1, 105] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ,其中 nums[i] 是节点 i 的基因值,且基因值 互不相同 。
请你返回一个数组 ans ,长度为 n ,其中 ans[i] 是以节点 i 为根的子树内 缺失 的 最小 基因值。
节点 x 为根的 子树 包含节点 x 和它所有的 后代 节点。
提示:
- n == parents.length == nums.length
- 2 <= n <= 10^5
- 对于 i != 0 ,满足 0 <= parents[i] <= n - 1
- parents[0] == -1
- parents 表示一棵合法的树。
- 1 <= nums[i] <= 10^5
- nums[i] 互不相同
示例:
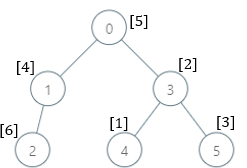
输入:parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
输出:[7,1,1,4,2,1]
解释:每个子树答案计算结果如下:
- 0:子树内包含节点 [0,1,2,3,4,5] ,基因值分别为 [5,4,6,2,1,3] 。7 是缺失的最小基因值。
- 1:子树内包含节点 [1,2] ,基因值分别为 [4,6] 。 1 是缺失的最小基因值。
- 2:子树内只包含节点 2 ,基因值为 6 。1 是缺失的最小基因值。
- 3:子树内包含节点 [3,4,5] ,基因值分别为 [2,1,3] 。4 是缺失的最小基因值。
- 4:子树内只包含节点 4 ,基因值为 1 。2 是缺失的最小基因值。
- 5:子树内只包含节点 5 ,基因值为 3 。1 是缺失的最小基因值。
Solution
一开始看到这个题目,就想到了 dfs序 + 线段树的解法。 dfs 序出来之后,必须以 dfs 序的区间来建立线段树,并进行更新处理,然后区间查询(每个节点都有一个区间),但是需要求的是 “缺失 的 最小 基因值”,用 dfs 序建立出来的线段树无法完成这个值更新以及查询操作。而用 每个值来建立线段树的话,又无法用 dfs 序查询,一时间就陷入这个解法里出不来了。。
官方题解做法:
做法1:
- dfs,用 set 记录每个子树的值的集合,然后不断向上合并,在合并时,总是从小的集合往大的集合进行合并(小大合并 Small to large),这样复杂度可以做到 O(nlogn)
- 记录每个子节点的 “缺失 的 最小 基因值”,当前节点从所有子节点中取最大的 “缺失 的 最小 基因值”,然后再在 set 里面判断一下,当前集合里(多了当前节点的值)是否包含这个 “缺失 的 最小 基因值”,如果是的话,则自增至不在 set 里面为止(动态规划的思想)
做法2:
- 注意题目的提示:1 <= nums[i] <= 10^5;nums[i] 互不相同。这说明了必定有一个节点 x 的 nums 值为1,从根节点到 x 节点的缺失基因值需要查询外,其余节点的缺失基因值都是1
- 从 x 节点开始查询,遍历 x 节点的所有子节点的值,存储到 set 里面,然后找出 “缺失 的 最小 基因值”,然后再查询父节点的值。类似做法1的第2点一样,父节点从所有子节点中取最大的 “缺失 的 最小 基因值”,不然会超时。。输上每个节点只需要遍历一遍,因此复杂度为O(n)
Code
// 做法1
class Solution {
int N = 100040;
int M = 400040;
int[] fst = new int[N], vv = new int[M], nxt = new int[M];
int e, n;
int[] ans;
void init() {
for (int i = 0; i <= n; ++i) fst[i] = -1;
e = 0;
ans = new int[n];
Arrays.fill(ans, 0);
}
void add(int u, int v) {
vv[e] = v;
nxt[e] = fst[u];
fst[u] = e++;
}
Set<Integer> dfs(int u, int p, int[] nums) {
Set<Integer> set = new TreeSet<>();
set.add(nums[u]);
ans[u] = 1;
for (int i = fst[u]; i != -1; i = nxt[i]) {
int v = vv[i];
if (v == p) continue;
Set<Integer> ss = dfs(v, u, nums);
ans[u] = Math.max(ans[u], ans[v]);
if (set.size() >= ss.size()) {
set.addAll(ss);
} else {
ss.addAll(set);
set = ss;
}
}
while (set.contains(ans[u])) {
ans[u]++;
}
return set;
}
public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
n = parents.length;
init();
for (int i = 1; i < n; ++i) {
add(parents[i], i);
}
dfs(0, -1, nums);
return ans;
}
}
//做法2
class Solution {
private HashSet<Integer>[] hashSet;
private HashSet<Integer> set;
private boolean[] vis;
void dfs(int u, int[] nums) {
set.add(nums[u]);
vis[u] = true;
for (Integer v : hashSet[u]) {
if (v == -1 || vis[v]) {
continue;
}
dfs(v, nums);
}
}
public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
int n = parents.length;
hashSet = new HashSet[n];
vis = new boolean[n];
for (int i = 0; i < n; ++i) {
hashSet[i] = new HashSet<>();
}
set = new HashSet<>();
Arrays.fill(vis, false);
for (int i = 1; i < n; ++i) {
hashSet[parents[i]].add(i);
}
int[] ans = new int[n];
Arrays.fill(ans, 1);
int x = -1;
for (int i = 0; i < n; ++i) {
if (nums[i] == 1) {
x = i;
break;
}
}
while (x != -1) {
dfs(x, nums);
while (set.contains(ans[x])) {
ans[x]++;
}
if (parents[x] != -1) {
ans[parents[x]] = ans[x];
}
x = parents[x];
}
return ans;
}
}